Skip to main content

Torque Ratios

The performance of the motor is sometimes expressed in terms of comparison of various torques such as full load torque, starting torque and maximum torque. The comparison is obtained by finding out ratios of these torques.
1.1 Full load and Maximum Torque Ratio
In general,        Tα (s E22 R2)/(R22 +(s X2)2)  
Let                     sf  = Full load slip
...                       TF.L. α (sf  E22 R2)/(R22 +(sf  X2)2)  
and                    sm = Slip for maximum torque Tm 
...                       Tm  α (sm  E22 R2)/(R22 +(sf  X2)2)

       Dividing both numerator and denominator by X22 we get,
But                       R2/X2 = sm 
                            TF.L./Tm  = (sf  x 2 sm2)/(sm x (sm2+ sf2))
                             TF.L./Tm   = (2 sf  sm)/(sm2 + sf2)
1.1 Starting Torque and Maximum Torque Ratio
       Against starting with torque equation as,
                           T α  (s E22 R2)/(R22 +(s X2)2)  
Now for Tst,        s =1
                           Tst  α   (E22 R2)/(R22 +( X2)2)
While for Tm,       s = sm
 
       Dividing both numerator and denominator by X22 we get,
      Substituting             R2/X2 = sm
 
       Infact using the same method, ratio of any two torques at two different slip values can be obtained.
       Sometimes using the relation, R2 = a X2 the torque ratios are expressed interms of constant a as,
                            TF.L./Tm  = (a sf )/(a2+ sf2)
and                       Tst/Tm  = 2 a/ (1 + a2)
where                    a = R2/X2 = sm
Example 1 : A 24 pole, 50 Hz, star connected induction motor has rotor resistance of 0.016 Ω per phase and rotor reactance of 0.265 Ω per phase at standstill. It is achieving its full load torque at a speed of 247 r.p.m. Calculate the ratio of 
i) Full load torque to maximum torque   ii) starting torque to maximum torque
Solution : Given values are,
   P = 24,   f = 50 Hz,       R2 = 0.016 Ω,   X2 = 0.265 Ω,     N = 247 r.p.m.
               Ns  = 120f / P = (120x50)/24 = 250 r.p.m.
                sf  = (Ns  - N)/Ns  = (250-247)/250 = 0.012 = Full load slip
                 sm = R2/X2 = 0.016/0.265 = 0.06037
i)              TF.L./Tm  = (2 sm sf )/(sm2+ sf2) = (2 x 0.06037 x 0.012)/(0.060372 + 0.0122)
ii)              Tst/Tm  = (2 sm )/(1 + sm2) = (2 x 0.06037)/(1 + 0.060372) = 0.1203

Labels

Labels:

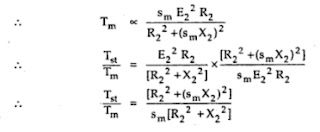
Comments

Post a Comment

Comment Policy
We’re eager to see your comment. However, Please Keep in mind that all comments are moderated manually by our human reviewers according to our comment policy, and all the links are nofollow. Using Keywords in the name field area is forbidden. Let’s enjoy a personal and evocative conversation.

Popular posts from this blog

Transformer multiple choice questions part 1

Hello Engineer's Q.[1] A transformer transforms (a) frequency (b) voltage (c) current (d) voltage and current Ans : D Q.[2] Which of the following is not a basic element of a transformer ? (a) core (b) primary winding (c) secondary winding (d) mutual flux. Ans : D Q.[3] In an ideal transformer, (a) windings have no resistance (b) core has no losses (c) core has infinite permeability (d) all of the above. Ans : D Q.[4] The main purpose of using core in a transformer is to (a) decrease iron losses (b) prevent eddy current loss (c) eliminate magnetic hysteresis (d) decrease reluctance of the common magnetic circuit. Ans :D Q.[5] Transformer cores are laminated in order to (a) simplify its construction (b) minimize eddy current loss (c) reduce cost (d) reduce hysteresis loss. Ans : B Q.[6] A transformer having 1000 primary turns is connected to a 250-V a.c. supply. For a secondary voltage of 400 V, the number of secondary turns should be (a) 1600 (b) 250 (c) 400 (d) 1250 A...
4 comments
Read more

Condition for Maximum Power Developed In Synchronous Motor

The value of δ for which the mechanical power developed is maximum can be obtained as, Note : Thus when R a is negligible, θ = 90 o for maximum power developed. The corresponding torque is called pull out torque. 1.1 The Value of Maximum Power Developed        The value of maximum power developed can be obtained by substituting θ = δ in the equation of P m .        When R a is negligible,     θ = 90 o  and cos (θ) = 0 hence, . . .               R a = Z s cosθ   and X s = Z s sinθ        Substituting   cosθ = R a /Z s in equation (6b) we get,         Solving the above quadratic in E b we get,        As E b is completely dependent on excitation, the equation (8) gives the excitation limits for a...
Post a Comment
Read more

Armature Voltage Control Method or Rheostatic Control of dc motor

Speed Control of D.C. Shunt Motor (Part2)  2. Armature Voltage Control Method or Rheostatic Control        The speed is directly proportional to the voltage applied across the armature. As the supply voltage is normally constant, the voltage across the armature can be controlled by adding a variable resistance in series with the armature as shown in the Fig. 1. Fig. 1 Rheostat control of shunt motor        The field winding is excited by the normal voltage hence I sh is rated and constant in this method. Initially the reheostat position is minimum and rated voltage gets applied across the armature. So speed is also rated. For a given load, armature current is fixed. So when extra resistance is added in the armature circuit, I a remains same and there is voltage drop across the resistance added ( I a R). Hence voltage across the armature decreases, decreasing the speed below normal value. By varyi...
Post a Comment
Read more