Skip to main content

Power Flow in an Induction Motor

Induction motor converts an electrical power supplies to it into mechanical power. The various stages in this conversion is called power flow in an inductor motor.
       The three phase supply given to the stator is the net electrical input to the motor. If motor power factor is cos Φ and VL, IL are line values of supply voltage and current drawn, then net electrical supplied to the motor can be calculated as,

       This is nothing but the stator input.
       The part of this power is utilised to supply the losses in the stator which are stator core as well as copper losses.
       The remaining power is delivered to the rotor magnetically through the air gap with the help of rotating magnetic field. This is called rotor input denoted as P2.

      The rotor is not able to convert its entire input to the mechanical as it has to supply rotor losses. The rotor losses are dominantly copper losses as rotor iron losses are very small and hence generally neglected. So rotor losses are rotor copper losses denoted as Pc.

       where     I2r = Rotor current per phase in running condition
                     R2  = Rotor resistance per phase.
       After supplying these losses, the remaining part of P2 is converted into mechanical which is called gross mechanical power developed by the motor denoted as Pm.

       Now this power, motor tries to deliver to the load connected to the shaft. But during this mechanical transmission, part of Pm is utilised to provide mechanical losses like friction and windage.
       And finally the power is available to the load at the shaft. This is called net output of the motor denoted as Pout. This is also called shaft power.

       The rating of the motor is specified in terms of value of Pout when load condition is full load condition.
       The above stages can be shown diagrammatically called power flow diagram of an induction motor.
       This is shown in the Fig.1.
Fig. 1 Power flow diagram

       From the power flow diagram we can define,


                                                         =  Pm / P2
Labels:

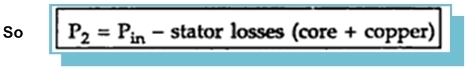
Comments

Post a Comment

Comment Policy
We’re eager to see your comment. However, Please Keep in mind that all comments are moderated manually by our human reviewers according to our comment policy, and all the links are nofollow. Using Keywords in the name field area is forbidden. Let’s enjoy a personal and evocative conversation.

Popular posts from this blog

Transformer multiple choice questions part 1

Hello Engineer's Q.[1] A transformer transforms (a) frequency (b) voltage (c) current (d) voltage and current Ans : D Q.[2] Which of the following is not a basic element of a transformer ? (a) core (b) primary winding (c) secondary winding (d) mutual flux. Ans : D Q.[3] In an ideal transformer, (a) windings have no resistance (b) core has no losses (c) core has infinite permeability (d) all of the above. Ans : D Q.[4] The main purpose of using core in a transformer is to (a) decrease iron losses (b) prevent eddy current loss (c) eliminate magnetic hysteresis (d) decrease reluctance of the common magnetic circuit. Ans :D Q.[5] Transformer cores are laminated in order to (a) simplify its construction (b) minimize eddy current loss (c) reduce cost (d) reduce hysteresis loss. Ans : B Q.[6] A transformer having 1000 primary turns is connected to a 250-V a.c. supply. For a secondary voltage of 400 V, the number of secondary turns should be (a) 1600 (b) 250 (c) 400 (d) 1250 A
4 comments
Read more

Condition for Maximum Power Developed In Synchronous Motor

The value of δ for which the mechanical power developed is maximum can be obtained as, Note : Thus when R a is negligible, θ = 90 o for maximum power developed. The corresponding torque is called pull out torque. 1.1 The Value of Maximum Power Developed        The value of maximum power developed can be obtained by substituting θ = δ in the equation of P m .        When R a is negligible,     θ = 90 o  and cos (θ) = 0 hence, . . .               R a = Z s cosθ   and X s = Z s sinθ        Substituting   cosθ = R a /Z s in equation (6b) we get,         Solving the above quadratic in E b we get,        As E b is completely dependent on excitation, the equation (8) gives the excitation limits for any load for a synchronous motor. If the excitation exceeds this limit, the motor falls out of step. 1.2 Condition for Excitation When Motor Develops ( P m ) R max        Let us find excitation condition for maximum power developed. The excitation
Post a Comment
Read more

Effect of Slip on Rotor Parameters : Part2

Effect of Slip on Rotor Parameters 2. Effect of Slip on Magnitude of Rotor Induced E.M.F        We have seen that when rotor is standstill, s  = 1, relative speed is maximum and maximum e.m.f. gets induced in the rotor. Let this e.m.f. be,                 E 2 = Rotor induced e.m.f. per phase on standstill condition         As rotor gains speed, the relative speed between rotor and rotating magnetic field decreases and hence induced e.m.f. in rotor also decreases as it is proportional to the relative speed N s - N. Let this e.m.f. be,                E 2r = Rotor induced e.m.f. per phase in running condition  Now        E 2r α N s while E 2r α N s - N        Dividing the two proportionality equations,               E 2r /E 2 = ( N s - N)/N s    but (N s - N)/N = slip s               E 2r /E 2 = s               E 2r = s E 2        The magnitude of the induced e.m.f in the rotor also reduces by slip times the
Post a Comment
Read more