Skip to main content

Characteristics of D.C. Shunt Motor

i) Torque - Armature current characteristics
       For a d.c. motor                 T α  Φ Ia
       For a constant values of Rsh and supply voltage V, Ish is also constant and hence flux is also constant.
...              Ta  α Φ Ia 
       The equation represents a straight line, passing through the origin, as shown in the Fig. 1. Torque increases linearly with armature current. It is seen earlier that armature current is decided by the load. So as load increases, armature current increases, increasing the torque developed linearly.
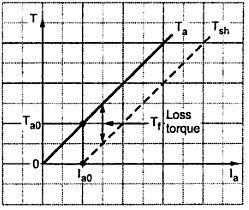Fig. 1  T Vs Ia for shunt motor
       Now if shaft torque is plotted against armature current, it is known that shaft torque is less than the armature torque and the difference between the two is loss torque Tf  as shown. On no load Tsh = 0 but armature torque is present which is just enough to overcome stray losses shown as Ta0. The current required is Ia0 on no load to produce Ta0 and hence Tsh graph has an intercept of Ia0 on the current axis.
       To generate high starting torque, this type of motor requires a large value of armature current at start. This may damage the motor hence d.c. shunt motors can develop moderate starting torque and hence suitable for such applications where starting torque requirement is moderate.
ii) Speed - Armature current characteristics 
       From the speed equation we get,
       N α (V - Ia  Ra)/Φ
             αV - Ia  Ra     as Φ is constant
       So as load increases, the armature current increases and hence drop Ia  Ra also increases.
       Hence for constant supply voltage, V - Ia  Ra decreases and hence speed reduces. But as  Ra is very small, for change in Ia from no load to full load, drop Ia Ra is very small and hence drop in speed is also not significant from no load to full load.
Fig. 2  N Vs Ia for shunt motor
       So the characteristics is slightly droping as shown in the Fig. 2.
       But for all practical purposes these type of motors are considered to be a constant speed motors.
iii) Speed - Torque characteristics
       These characteristics can be derived from the above two characteristics. This graph is similar to speed-armature current characteristics as torque is proportional to the armature current. This curve shows that the speed almost remains constant through torque changes from no load to full load conditions. This is shown in the Fig. 3.
Fig. 3  N Vs T for shunt motor
Labels:

Comments

Post a Comment

Comment Policy
We’re eager to see your comment. However, Please Keep in mind that all comments are moderated manually by our human reviewers according to our comment policy, and all the links are nofollow. Using Keywords in the name field area is forbidden. Let’s enjoy a personal and evocative conversation.

Popular posts from this blog

Demagnetising and Cross Magnetizing Conductors

The conductors which are responsible for producing demagnetizing and distortion effects are shown in the Fig.1. Fig. 1        The brushes are lying along the new position of MNA which is at angle θ  from GNA. The conductors in the region AOC = BOD = 2θ  at the top and bottom of the armature are carrying current in such a direction as to send the flux in armature from right to left. Thus these conductors are in direct opposition to main field and called demagnetizing armature conductors.         The remaining armature conductors which are lying in the region AOD and BOC carry current in such a direction as to send the flux pointing vertically downwards i.e. at right angles to the main field flux. Hence these conductors are called cross magnetizing armature conductors which will cause distortion in main field flux.        These conductors are shown in the Fig. 2 Fig. 2  ...
Post a Comment
Read more

Armature Voltage Control Method or Rheostatic Control of dc motor

Speed Control of D.C. Shunt Motor (Part2)  2. Armature Voltage Control Method or Rheostatic Control        The speed is directly proportional to the voltage applied across the armature. As the supply voltage is normally constant, the voltage across the armature can be controlled by adding a variable resistance in series with the armature as shown in the Fig. 1. Fig. 1 Rheostat control of shunt motor        The field winding is excited by the normal voltage hence I sh is rated and constant in this method. Initially the reheostat position is minimum and rated voltage gets applied across the armature. So speed is also rated. For a given load, armature current is fixed. So when extra resistance is added in the armature circuit, I a remains same and there is voltage drop across the resistance added ( I a R). Hence voltage across the armature decreases, decreasing the speed below normal value. By varyi...
Post a Comment
Read more

Characteristics of Separately Excited D.C. Generators

The characteristics is separately excited d.c. generator are divided into two types, 1) Magnetization   and         2) Load characteristics. 1.1 Magnetization or Open Circuit Characteristics         The arrangement to obtain this characteristics is shown in the Fig. 1. Fig. 1  Obtaining O.C.C. of separately excited generator        The rheostat as a potential driver is used to control the field current and the flux. It is varied from zero and is measured on ammeter connected.        E o  = (ΦPNZ) / (60A)        As I f is varied, then Φ change and hence induced e.m.f. E o  also varies. It is measured on voltmeter connected across armature. No Load is connected to machine, hence characteristics are also called no load characteristics which is graph of E o  against field current I f as sho...
Post a Comment
Read more