Skip to main content

Winding Pitches

Now we will consider the definitions of different types of winding pitches, required in the design of the armature winding.
1.1 Back Pitch 
       The distance which is measured interns of armature conductors i.e. between top and bottom coil sides of a coil measured around the back of the armature i.e. away from the commutator is called back pitch and is denoted by . It is measured interms of coil sides.
Note : Since it is difference between odd and even number, it is always odd number.
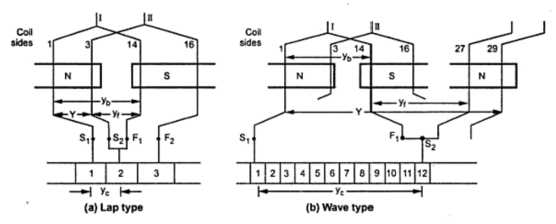
       The size of the coil is decided by the back pitch. The back pitch is normally equal to coilsides per pole. It is shown for lap and wave type of winding in the Fig. 1.
Fig. 1
       The back pitch for the winding shown in the Fig. 1 is yb = 14 - 1 = 13 as coilsides 1and 14 are of coil number 1.
1.2 Front Pitch
       It is defined as the distance measured between two coilsides which are connected to some commutator segment. It is denoted by yf. The front pitch for the winding shown in the Fig. 1 is  yf = 14 - 3 = 11. This is front pitch for lap winding while for wave winding yf = 27 - 14 = 13. The front pitch for both lap and wave type winding is odd. If for a lap winding the connections are traced then the movement is backwards (coil side 14 to coil side 3). Hence the type of winding can be determined from front pitch and it does not affect the size of coils.
1.3 Winding Pitch
       It is defined as the distance between the starts of two consecutive coils measured in terms of coil sides. It is denoted by Y.
       For lap winding,       Y = yb - yf
       For Wave winding,   Y = yb + yf
       For the lap winding shown in the Fig. 1 the winding pitch is Y = 13 - 11 = 2 while for wave winding Y = 13 + 13 = 26. It is also the distance round the armature between two consecutive conductors. Practically, coil pitches or winding pitches as low as eight tenths of a pole pitch are employed without much reduction in emf.
Note : Fractional pitches windings are intentionally used so as to achieve saving in copper of the end connections and for improvement in commutation.
1.4 Commutator Pitch
       It is defined as the distance between the two commutator segments to which the two ends i.e. starts and finish of a coil are connected. It is measured in terms of commutator segments and it is denoted by yc. For the windings shown in the Fig. 1.
       yc = 2 - 1 = 1     for simplex lap winding
       yc= 12 - 1 = 11 for simplex wave winding
       For lap winding is the difference between yb and yf while for wave winding yc is the sum of yb and yf. The number of bars between the coil leads is commutator pitch. In general yc is the 'plex' of lap wound armature. It is 1, 2, 3 for simplex, duplex, triplex lap windings respectively.
       On tracing through simplex lap winding,a segment adjacent to the first one is reached after traversing through one coil. For simplex wave winding, the adjacent segment is reached after traversing through P/2 coils.
Labels:

Comments

Post a Comment

Comment Policy
We’re eager to see your comment. However, Please Keep in mind that all comments are moderated manually by our human reviewers according to our comment policy, and all the links are nofollow. Using Keywords in the name field area is forbidden. Let’s enjoy a personal and evocative conversation.

Popular posts from this blog

Practical Commutation

The e.m.f. induced in each coil of armature is alternating in nature. If load is connected, the current flowing will also be alternating. But the flow of current in a d.c. generator must be undirectional. This can be achieved by the use of commutator. When the armature conductors are under the influence of one pole they carry current in one direction whereas the current is reversed when the conductors are under the influence of other pole. This reversal of current takes place along the magnetic neutral axis. Fig. 1 Note : The reversal of current is likely to take place in short interval when a coil is short circuited by a brush so that transfer of current from one direction to other is carried out without any sparking. This process is called commutation.        Thus a process by which current in the short circuited coil is reversed while it crosses the MNA is called commutation. The time during which the coil remains short circuited is known as...
1 comment
Read more

Demagnetising and Cross Magnetizing Conductors

The conductors which are responsible for producing demagnetizing and distortion effects are shown in the Fig.1. Fig. 1        The brushes are lying along the new position of MNA which is at angle θ  from GNA. The conductors in the region AOC = BOD = 2θ  at the top and bottom of the armature are carrying current in such a direction as to send the flux in armature from right to left. Thus these conductors are in direct opposition to main field and called demagnetizing armature conductors.         The remaining armature conductors which are lying in the region AOD and BOC carry current in such a direction as to send the flux pointing vertically downwards i.e. at right angles to the main field flux. Hence these conductors are called cross magnetizing armature conductors which will cause distortion in main field flux.        These conductors are shown in the Fig. 2 Fig. 2  ...
Post a Comment
Read more

Armature Voltage Control Method or Rheostatic Control of dc motor

Speed Control of D.C. Shunt Motor (Part2)  2. Armature Voltage Control Method or Rheostatic Control        The speed is directly proportional to the voltage applied across the armature. As the supply voltage is normally constant, the voltage across the armature can be controlled by adding a variable resistance in series with the armature as shown in the Fig. 1. Fig. 1 Rheostat control of shunt motor        The field winding is excited by the normal voltage hence I sh is rated and constant in this method. Initially the reheostat position is minimum and rated voltage gets applied across the armature. So speed is also rated. For a given load, armature current is fixed. So when extra resistance is added in the armature circuit, I a remains same and there is voltage drop across the resistance added ( I a R). Hence voltage across the armature decreases, decreasing the speed below normal value. By varyi...
Post a Comment
Read more